Statistik II (VL+UE) + Intensivübung Statistik
![]()
![]()
- Kategorie
- Bachelor
- Lehrende(r)
- VL: B. Lopez Cabrera, UE: T. Ermakova, S. Klinke, D. Prastyod, TU: I. Karpenka, F. Schulz, T. Sydorenko, N.N., UEST: S. Klinke
[ Folien, Aufgaben & Formelsammlung | Statistics (CD-ROM) | Vorlesungsinhalte | Vorlesungsdisposition | Empfohlene Literatur]
Folien, Aufgaben & Formelsammlung
Diese Materialien laden Sie sich bitte aus dem Moodle-System der Humboldt-Universität. Falls sie neu im Moodle-System sind, müssen sie sich einen neuen Account anlegen und eine gültige E-Mail-Adresse besitzen. Nach der Neuanlegung des Accounts wird Ihnen das Passwort auf die angebene E-Mailadresse zugeschickt.
Statistik - Wissenschaftliche Datenanalyse leicht gemacht
Statistics – Multilingual Edition (4-sprachig: Deutsch, Englisch, Spanisch, Französisch)
Wissenschaftliche Datenanalyse leicht gemacht:
Die interaktiv konzipierte CD-ROM bietet ein neuartiges Tool zur Einführung in die Welt der Statistik. Sie dient (als Nachfolger von "MM*Stat") als Skript für Statistik I und II. In zwölf Kapiteln werden alle klassischen Teilgebiete der deskriptiven und induktiven Statistik vollständig erklärt. Durch eine Vielfalt an Beispielen und interaktiven Recheneinheiten wird die Materie leichter erfassbar. Multiple-Choice-Fragen ermöglichen eine Überprüfung des gelernten Stoffes. Mit Bonusmaterial: Der komplette Kurs auch in Spanisch und Französisch auf der CD-ROM! Weitere Informationen und Bestellen unter www.mhsg.de oder direkt bei
Multimedia Hochschulservice Berlin GmbH
c/o Technische Universität Berlin
Raum EN 053
Einsteinufer 17d
10587 Berlin
Sprechzeiten: Mo.-Fr. 09:00-17:00 Uhr
Vorlesungsinhalte
Grundlage vieler Methoden der Statistik ist die Wahrscheinlichkeitsrechnung. Ihr Untersuchungsgegenstand sind Zufallsexperimente und ihre möglichen Ausgänge (Ereignisse). Die Chance des Eintretens von Ereignissen wird durch die Wahrscheinlichkeit charakterisiert. Wesentliche Wahrscheinlichkeitsbegriffe und wichtige Sätze für die Berechnung von Wahrscheinlichkeiten (z.B. Additionssatz, Multiplikationssatz, Satz der totalen Wahrscheinlichkeit und Theorem von Bayes) werden eingeführt.
Das Erkenntnisziel der Statistik manifestiert sich in einem Doppelcharakter, der bei allen Anwendungen statistischer Verfahren beachtet werden muss: Die deskriptive (beschreibende) Statistik umfasst statistische Verfahren, die die Erhebung, Aufbereitung und Auswertung von Daten entsprechend einer gegebenen Zielstellung beinhalten und die der quantitativen Beschreibung der beobachteten Massenerscheinungen dienen. Erzielte Ergebnisse und Aussagen beziehen sich grundsätzlich nur auf die untersuchte Datenmenge.
Die induktive (schließende) Statistik umfasst Verfahren, die die Übertragung von Ergebnissen aus untersuchten Teilgesamtheiten auf die Grundgesamtheit erlauben, wobei dieser Rückschluss unter Vorgabe einer gewissen Präzision vorgenommen werden soll.
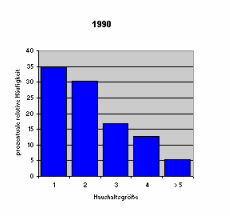
Variablen, ihre Verteilungen und Parameter bilden den Einstieg in die Statistik. Zum einen sind aus deskriptiver Sicht die empirischen Häufigkeitsverteilungen zu betrachten. Zum anderen sind Zufallsvariablen, ihre Wahrscheinlichkeitsverteilungen bzw. Dichtefunktion+ Intensivübung Statistiken unentbehrlich für die induktive Statistik.
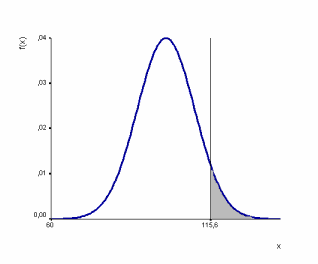 Neben den beobachteten Verteilungen gibt es wichtige Verteilungsmodelle. Dazu gehören: diskrete und stetige Gleichverteilung, Binomialverteilung, hypergeometrische Verteilung, Poisson-Verteilung, Exponentialverteilung, Normalverteilung, Chi-Quadrat-Verteilung, t-Verteilung und F-Verteilung.
Neben den beobachteten Verteilungen gibt es wichtige Verteilungsmodelle. Dazu gehören: diskrete und stetige Gleichverteilung, Binomialverteilung, hypergeometrische Verteilung, Poisson-Verteilung, Exponentialverteilung, Normalverteilung, Chi-Quadrat-Verteilung, t-Verteilung und F-Verteilung.
Stichproben sind die Grundlage vieler statistischer Analysen, so dass sich ein Überblick über die Stichprobentheorie anschließt. Grundbegriffe wie Grundgesamtheit, Stichprobe, Stichprobenvariable und Stichprobenfunktion werden erläutert. Von den vielen existierenden Stichprobenfunktionen werden der Stichprobenmittelwert, der Stichprobenanteilswert und die Stichprobenvarianz mit der jeweiligen Verteilung behandelt.
Um aus den Ergebnissen einer Stichprobe auf die entsprechenden Parameter der Grundgesamtheit schließen zu können, werden Schätzverfahren benötigt. Es wird gezeigt, wie man zu Schätzfunktionen mit wünschenswerten Eigenschaften (Erwartungstreue, Effizienz, Konsistenz) gelangt. Die Punktschätzung des Erwartungswertes der Grundgesamtheit und des Anteilswertes einer dichotomen Grundgesamtheit wird durch ihre Intervallschätzung (Konstruktion von Konfidenzintervallen) ergänzt.
Der Frage, wie Hypothesen über die Grundgesamtheit aufgrund einer Stichprobenuntersuchung statistisch geprüft werden, ist Gegenstand der statistischen Testtheorie. Nach der Darlegung der Grundgedanken statistischen Testens werden exemplarisch zwei Parametertests (Test über den Erwartungswert und Test über den Anteilswert) sowie ein Test zur Prüfung einer Annahme über die Verteilung einer Zufallsvariablen behandelt.
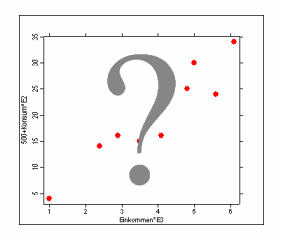 Da man sich bei vielen statistischen Untersuchungen gleichzeitig für mehrere Variablen interessiert, wird exemplarisch für eine solche mehrdimensionale Betrachtungsweise die zweidimensionale Häufigkeits- bzw. Wahrscheinlichkeitsverteilung behandelt. Randverteilungen, bedingte Verteilungen, Unabhängigkeit von Variablen und die Messung von Zusammenhängen von zwei Variablen (Korrelation, Kontingenz) sind Problemkreise, die hierbei eine entscheidende Rolle spielen.
Da man sich bei vielen statistischen Untersuchungen gleichzeitig für mehrere Variablen interessiert, wird exemplarisch für eine solche mehrdimensionale Betrachtungsweise die zweidimensionale Häufigkeits- bzw. Wahrscheinlichkeitsverteilung behandelt. Randverteilungen, bedingte Verteilungen, Unabhängigkeit von Variablen und die Messung von Zusammenhängen von zwei Variablen (Korrelation, Kontingenz) sind Problemkreise, die hierbei eine entscheidende Rolle spielen.
Die Schätzung der mittleren statistischen Abhängigkeit einer abhängigen Variablen Y von einer Reihe von erklärenden Variablen X1, X2, ..., Xm auf Basis einer Zufallsstichprobe ist Gegenstand der Regressionsanalyse. Die Behandlung der Regressionsanalyse wird auf die einfache lineare Regression beschränkt, deren Parameter mittels der Methode der kleinsten Quadrate geschätzt werden. Die Güte der geschätzten Regressionsfunktion, Tests der Parameter und Konfidenzintervalle sind weitere wichtige Bestandteile der Regressionsanalyse.
Der letzte Abschnitt der Lehrveranstaltung ist der Zeitreihenanalyse gewidmet. Aufgabe der Zeitreihenanalyse ist es, die in den Beobachtungswerten einer Variablen enthaltenen systematischen Komponenten, wie z.B. Trend und Saisonschwankungen, heraus zu filtern. Dabei wird die Variable als Funktion der Zeit beschrieben. Auch für das geschätzte Zeitreihenmodell ist die Güte der Anpassung an die Beobachtungen zu überprüfen.
Vorlesungsdisposition "Statistik I + II"
1 Grundzüge der Wahrscheinlichkeitsrechnung
1.1 Zufallsexperimente und Ereignisse
1.2 Wahrscheinlichkeitsbegriffe
1.3 Additionssatz
1.4 Bedingte Wahrscheinlichkeit und unabhängige Ereignisse
1.5 Multiplikationssatz
1.6 Totale Wahrscheinlichkeit
1.7 Theorem von Bayes
2 Zufallsvariablen, ihre Verteilungen und Parameter
2.1 Zufallsvariablen und ihre Skalierung
2.2 Gruppierung von Variablenwerten
2.3 Verteilung von Zufallsvariablen
2.3.1 Diskrete Zufallsvariable (empirische Verteilung, Wahrscheinlichkeitsverteilung)
2.3.1 Stetige Zufallsvariable (empirische Verteilung, Wahrscheinlichkeitsdichte)
2.4 Parameter von Zufallsvariablen
2.4.1 Lageparameter (Mittelwerte)
2.4.1.1 Arithmetisches Mittel und Erwartungswert
2.4.1.2 Modus
2.4.1.3 Median und Quantile
2.4.1.4 Harmonisches Mittel
2.4.2. Streuungsparameter
2.4.2.1 Spannweite
2.4.2.2 Quartilsabstand
2.4.2.3 Mittlere absolute Abweichung
2.4.2.4 Varianz und Standardabweichung
2.4.3 Kommentare zu Lage- und Streuungsmaßen
3 Zweidimensionale Häufigkeits- bzw. Wahrscheinlichkeitsverteilungen
3.1 Diskrete Variablen
3.2 Stetige Variablen
3.3 Randverteilungen, bedingte Verteilungen und ihre Parameter
3.4 Unabhängige Variablen und Kovarianz
3.5 Maßzahlen für den Zusammenhang zweier Variablen
3.5.1 Zusammenhang zwischen metrisch skalierten Variablen
3.5.2 Zusammenhang zwischen ordinal skalierten Variablen
3.5.3 Zusammenhang zwischen nominal skalierten Variablen
4 Wichtige Verteilungsmodelle
4.1 Gleichverteilung
4.2 Binomialverteilung
4.3 Hypergeometrische Verteilung
4.4 Poisson - Verteilung
4.5 Exponentialverteilung
4.6 Normalverteilung
4.7 Zentraler Grenzwertsatz
4.8 Chi-Quadrat-Verteilung
4.9 t - Verteilung
4.10 F - Verteilung
5 Stichprobentheorie
5.1 Grundbegriffe
5.2 Stichprobenverteilungen
5.2.1 Verteilung des Stichprobenmittelwertes
5.2.2 Verteilung des Stichprobenanteilswertes
5.2.3 Verteilung der Stichprobenvarianz
6 Statistische Schätzverfahren
6.1 Schätzfunktionen
6.1.1 Grundbegriffe
6.1.2 Eigenschaften von Schätzfunktionen
6.1.3 Konstruktion von Schätzfunktionen
6.2 Intervallschätzung
6.2.1 Konfidenzintervall für den Erwartungswert μ
6.2.2 Konfidenzintervall für den Anteilswert π
6.2.3 Bestimmung des Stichprobenumfanges
7 Statistische Testverfahren
7.1 Grundbegriffe
7.2 Einige Testverfahren
7.2.1 Testverfahren für den Erwartungswert μ der Grundgesamtheit
7.2.2 Testverfahren für den Anteilswert π einer dichotomen Grundgesamtheit
7.2.3 Testverfahren für die Differenz der zweier Erwartungswerte
7.2.4 Chi-Quadrat-Anpassungstest
7.2.5 Chi-Quadrat-Unabhängigkeitstest
8 Regressionsanalyse
8.1 Das Regressionsproblem
8.2 Schätzung der Regressionsparameter
8.3 Bestimmtheit der Regression
8.4 Statistischer Test der Regressionsparameter
8.5 Konfidenzintervalle im Rahmen der Regressionsanalyse
9 Zeitreihenanalyse
9.1 Zeitreihe und ihre Komponenten
9.2 Geometrisches Mittel
9.3 Ermittlung des Trends einer Zeitreihe
9.3.1 Methode der gleitenden Durchschnitte
9.3.2 Methode der kleinsten Quadrate
9.4 Periodische Schwankungen
9.5 Einschätzung der Güte des Zeitreihenmodells
Empfohlene Literatur
| Sterne1 | Autor(en) | Jahr | Titel | Verlag |
|---|---|---|---|---|
| 3,5 | Bamberg, Baur | 2009 | Statistik | Oldenbourg, München |
| -- | Bamberg, Baur | 2007 | Statistik-Arbeitsbuch, Übungsaufgaben - Fallstudien - Lösungen | Oldenbourg,München |
| 4,1 | Bleymüller u.a. | 2008 | Statistik für Wirtschaftswissenschaftler | Verlag Franz Vahlen, München |
| 4,1 | Bleymüller u.a | 2007 | Statistische Formeln, Tabellen, Programme | Verlag Franz Vahlen, München |
| -- | Bohley | 2000 | Statistik | Oldenbourg, München |
| -- | Bohley | 1999 | Formeln, Rechenregeln, EDV und Tabellen zur Statistik | Oldenbourg, München |
| -- | Elpelt, Hartung | 2009 | Statistik: Lehr- und Handbuch der angewandten Statistik | Oldenbourg, München |
| 3,6 | Fahrmeir u.a. | 2009 | Statistik | Springer, Berlin |
| -- | Fahrmeir u.a. | 2008 | Arbeitsbuch Statistik | Springer, Berlin |
| -- | Hartung u.a. | 2009 | Statistik: Lehr- und Handbuch der angewandten Statistik | Oldenbourg, München |
| -- | Litz | 2003 | Statistische Methoden in den Wirtschafts- und Sozialwissenschaften | Oldenbourg Verlag, München, Wien |
| -- | Rinne | 2003 | Taschenbuch der Statistik. Für Wirtschafts- und Sozialwissenschaften (Gebundene Ausgabe) | Harri Deutsch, Frankfurt/M |
| -- | Schira, Joseph | 2009 | Statistische Methoden der VWL und BWL | Pearson Studium |
| -- | Schlittgen | 2008 | Einführung in die Statistik. Analyse und Modellierung von Daten | Oldenbourg, München |
| -- | Schwarze | 2009 | Grundlagen der Statistik 1: Beschreibende Verfahren | Verlag Neue Wirtschaftsbriefe, Herne, Berlin |
| -- | Schwarze | 2008 | Grundlagen der Statistik 2: Wahrscheinlichkeitsrechnung und induktive Statistik | Verlag Neue Wirtschaftsbriefe, Herne, Berlin |
| -- | Schwarze | 2008 | Aufgabensammlung zur Statistik | Verlag Neue Wirtschaftsbriefe, Herne, Berlin |
| -- | Vogel | 2005 | Beschreibende und schließende Statistik: Formeln, Definitionen, Erläuterungen, Stichwörter und Tabellen | Oldenbourg Verlag, München, Wien |
| -- | Vogel | 2001 | Beschreibende und schließende Statistik. Aufgaben und Beispiele | Oldenbourg Verlag, München, Wien |
| -- | Zöfel | 2003 | Statistik für Wirtschaftswissenschaftler im Klartext | Pearson |
1Die Sternezahl entspricht der Zahl der Sternchen bei amazon.de (Stand: 08.12.2009), min. 10 Bewertungen!
