Humboldt-Universität zu Berlin - High Dimensional Nonstationary Time Series

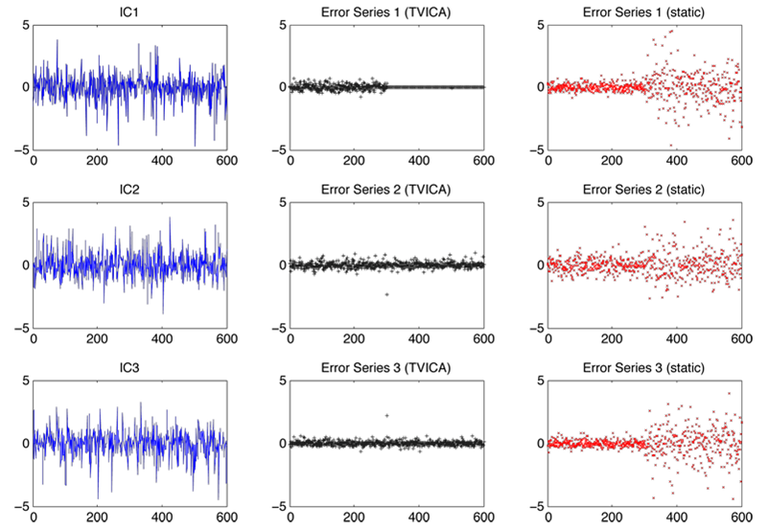
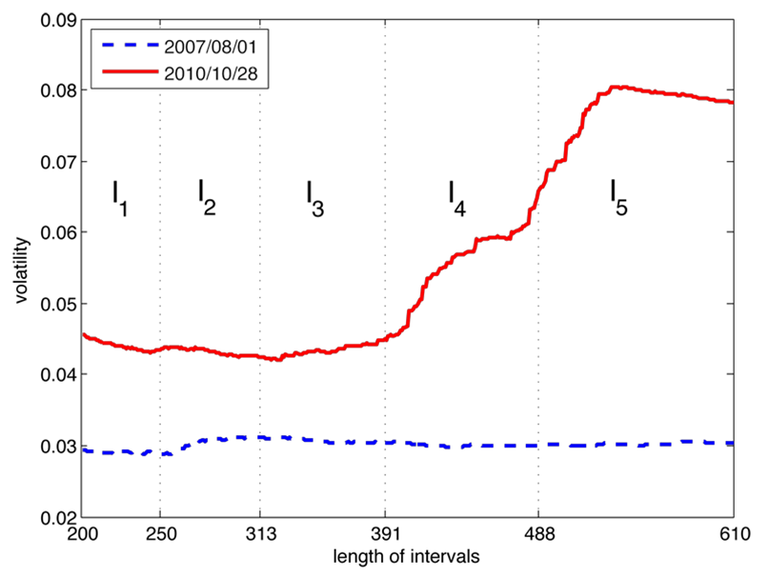
Statistical modelling for dynamic economic, finance and weather data in high dimensions requires a balanced combination of flexibility, interpretability and numerical tractability. Dimension reduction techniques for functional data analysis model and approximate smooth random functions by lower dimensional objects. The most prominent dimension reduction technique, Functional Principal Components Analysis, combines PCA and dimension reduction with pre-smoothing for effective dimensional space at fixed time horizon. In many applications the focus of interest lies not only in dimension reduction but also in the dynamic behaviour of the lower dimensional objects. Dynamic Semiparametric Factor Models (DSFM) simultaneously reduce dimensionality avoiding preliminary smoothing and consider the time structure of unknown random functions by means of inference based on their lower dimensional representation with flexible basis structures: the unknown nonparametric factors (Fengler et al., 2007; Park et al., 2009). The DSFM nests linear models which allow for time varying coefficients as a special case, such as Fan et. al (2007) or Yang et al. (2006). The main result is that one may proceed in inferential testing with the estimated factor loading process and does not need to know the (unobservable) time series. The choice of basis functions have been dealt with in Song et al. (2011) where also variable selection techniques are discussed.

 

A high-dimensional generalised varying coefficient regression model has been presented in Lee et al. (2011). An open question still is the choice of basis functions and other dimensionality parameters (e.g. bandwidth) in practical applications. The basis functions could, for example, include the shift, slope and twist as basic elements. In many situations the coefficients of the basis functions need to be constrained in order to allow for structural forms. Generalizations of the DSFM need to be studied Penalizations, such as LASSO (Least Absolute Shrinkage and Selection Operator) or SCAD (smoothly clipped Absolute Deviation), and more general convex contrasts (Bradic et al., 2011) will overcome the problem of overfitting. Furthermore we would like to analyse asymptotics of semiparametric factor dynamics and show that the difference of the inferences based on the estimated factor and the true factor is asymptotically negligible.

 

 

 

Coordination