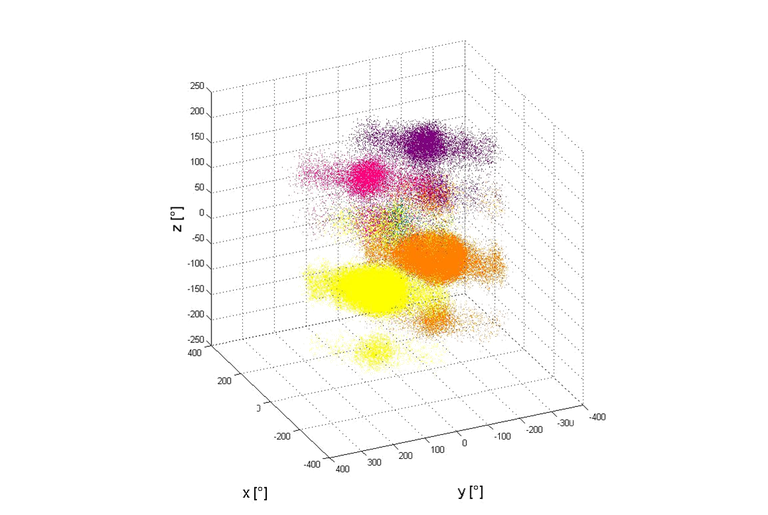A1 - Structuring high-dimensional time series
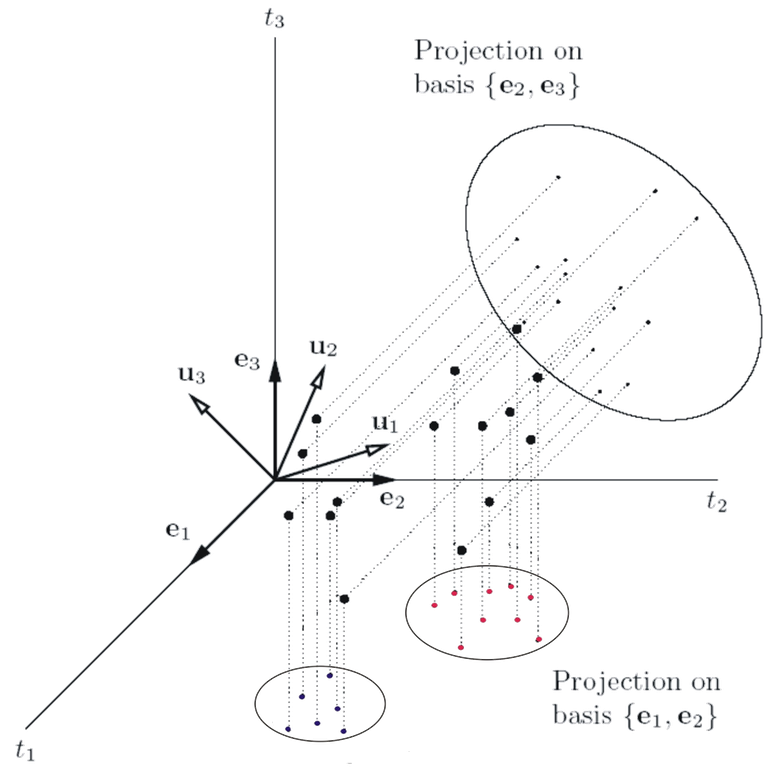
Modern statistical and econometric studies frequently face high dimensional time series. Examples come from financial, economic, climate data, functional data analysis, medical imaging and pharmacokinetics, among many others. The stylized feature of such data can be unknown dependence between components, time inhomogeneity in mean and in volatility, structural changes. Modeling and forecasting for such dynamic system requires understanding and recovery of its underlying structure.
The structural assumptions for the considered set of time series allow for reducing its dimensionality and complexity. Classical linear time series modeling fail to mimic many essential features of the data and nonlinear models with unknown link functions become more and more popular. An important example is provided by dynamic factors models; see Bathia, Yao, and Ziegelmann (2010), Pan and Yao (2008), Park et al (2007), with applications in modeling of implied volatility dynamics, Fengler, Härdle, Mammen (2007). Single- and multi-index modeling build another important class of nonlinear time series; see Xia (2008), Xia, Xu and Zhang (2010), Hristache et al (2001), Kong and Xia (2011).
Independent Components (ICA) provides another useful structural assumption about multidimensional time series; Hyvärinen et al (2001). It is widely used in engineering fields but also in econometric applications; Chen, Härdle, and Spokoiny (2007). An extension of ICA called Non-Gaussian Component Analysis; see Blanchard et al (2005), has been successfully applied to protein modeling in pharmacokinetics, Diederichs et al (2010).
Copula as a special form of dependency for multivariate data becomes one of the standard tools in Risk Management; Embrechts, McNeil, Straumann (2002), Giacomini, Härdle, and Spokoiny (2009).
Identifying the structural features of the multidimensional time series like cointegration or unit root behavior remains one of the most important topics in multiple time series analysis. See Lütkepohl (2005).
Coordination
- Zongwu Cai: His main interests are Econometrics, Quantitative Finance, Nonlinear Time Series. His research includes work in Theoretical and applied econometrics, quantitative finance and risk management, nonparametric curve estimation problems, nonlinear and non-stationary time series, panel data analysis.
- Ying Fang: His main interests are Econometrics, Applied Econometrics, Economy of China. His research includes work in nonparametric and semi-parametric method, panel data analysis, and instrumental variable selection.
- Wolfgang Härdle: His main interests are non- and semiparametrics statistics and econometrics. His research includes work in nonparametric modelling, local adaptive models, reduction techniques, stationary models, quantile regression.
- Yongmiao Hong: Econometrics, Time Series Analysis, Financial Econometrics,Chinese Economics. His research includes high dimensional data analysis, nonparametric finance.
- Ming Lin: His main interests are Monte Carlo Methods, self selection, dimension reduction methods. His research includes work in Monte Carlo algorithm, Bayesian statistics, nonparametric statistics.
- Vladimir Spokoiny: His main interests are non and semiparametric statistics, local adaptive method. His research includes work in high dimensional data analysis, statistical method in finance, nonlinear time series.