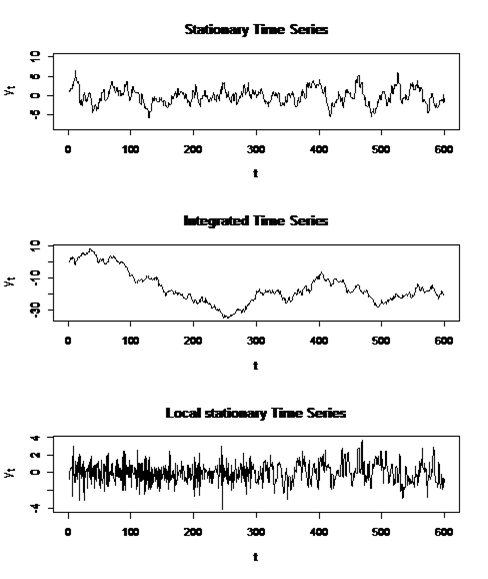Humboldt-Universität zu Berlin - High Dimensional Nonstationary Time Series

In recent years two main complementary strands of econometric/statistical literature have evolved which deal with nonlinear structural relations of unknown form of stochastically nonstationary underlying processes. First, there are methods which focus on long-term relations and generalize the concept of linear cointegration to non-and semiparametric versions thereof for a broad class of stationary and nonstationary processes. Second, adaptive methods concentrate on precise and accurate short-term forecasts. 

 

The evolution of these techniques has been driven by empirical necessity. A variety of studies with potentially non-stationary quantities have produced counterintuitive and contradictory results (see Campbell and Yogo (2006), Cai, Li and Park (2009), Xiao (2009)). This may be partly attributed to inappropriate standard econometric and statistical methods that restrict non-stationarity to unit root or long-memory ARFIMA types of nonstationarity and structural relations to linear or parametric type of cointegration models. 

 

Inference for nonparametric type of cointegration relations requires processes with a certain recurrence structure. In particular, this class of processes is general enough to contain stationary, long-memory, unit-root type or nearly integrated processes as sub-classes. Obtained asymptotic results for univariate and bivariate density and conditional mean type estimators are thus robust to nonstationarity (Karlsen et al., 2007 and Wang and Phillips, 2009a, 2009b). There are many open challenges in this field. In particular, clever dimension reduction methods and semiparametric models are needed to allow for general multivariate settings as in Schienle (2008). Furthermore, it is important to develop appropriate statistical tests for specific functional forms given underlying recurrent processes in order to check the validity of models from Economic and Financial theory. In contrast to conventional statistical tests, they would be valid also for non-stationary or nearly non-stationary covariates. To implement such tests, in particular, sophisticated techniques for a data-driven choice of bandwidth and suitable bootstrap methods are required. Moreover, in macroeconomic settings, a testing framework specifically for smooth structural changes when state variables are nonstationary would be an important tool. The prevalence of structural instability in macroeconomic time series relations or excess returns on international equity indices related to state variables has indeed been confirmed by numerous empirical studies in economics and finance (see e.g. Paye and Timmermann, 2006, Cai, 2007, Chen and Hong, 2009, all for stationary variables). But structural change might also result from nonstationary state variables, e.g., economic agents may change their production, consumption, savings and other patterns of behavior.

 

Adaptive Techniques become more and more important in various applications of time series analysis. Ignoring structural changes in the observed systems like economic or financial market may lead to wrong decisions like underestimation of the insurance or financial risks. Adaptive methods focus on detecting the largest interval of homogeneity where the hypothesis of certain parametric data structure does not contradict the observed data. The Berlin mathematical school gained some expertise in this area; see Mercurio and Spokoiny (2004), Spokoiny (2009). Recent extensions include local adaptive copulae; Giacomini et al (2009) and local adaptive quantile regression; Härdle et al (2011).

 

A new important challenge is extending the proposed adaptive approach to high dimensional dynamic systems. Here the adaptive techniques have to be combined with the methods of dimension reduction like Independent Component Analysis; Chen et al (2009), or NonGaussian Component Analysis; Blanchard et al (2005), Diederichs et all (2010).

 

 

 

Coordination